Question

Examine these points on line u and line v. Line u: (9, –8), (5, 4) Line v: (4, 2), (7, –7) How many points of intersection are there between line u and line v?

Answer 1

The correct answer is A: Zero

Explanation:

Answer 2

The line u and line v have no point of intersection because they are parallel lines

Explanation:

The slope of a straight line is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

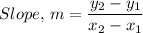
The slope of line u is (4 - (-8))/(5 - 9) = -3

The equation for line u is y - 4 = -3*(x - 5)

y = -3·x + 15 + 4 = 19 - 3·x

The slope for line v is (-7 - 2)/(7 - 4) = -3

The equation for the line v is y - 2 = -3*(x - 4)

∴ y = -3x + 12 + 2 = -3x + 14

y = 14 - 3·x

Therefore. line u and line v have the same slope and are therefore parallel and they do not intersect