Answer:
Year 2030.
Explanation
In 1997, Let Tim's age = X years
In 1997, Let Sue's age = Y years
After 5 years in 2002, Tim's age = (X+ 5) years
After 5 years in 2002, Sue's age = (Y + 5) years
Now, According to question,
X + Y = 32 (sum of their ages) .......(1)
Y = 32 - X
(X + 5) = 2 (Y + 5) .......(2)
Substituting the value of Y in (2)
X + 5 = 2 (32 - X + 5)
X + 5 = 2 (37 - X )
X + 5 = 74 - 2X
3X = 69
X = 69/3 = 23
Now ∵ Y = 32 - X and X = 23
∴ Y = 32 - 23 = 9
So, In 1997, Tim's age = 23 years and Sue's age = 9 years.
Let the year in which Sue's age will be three-fourth times of Tim's age be t.
Sue's age after t years = (9 + t) years.
Tim's age after t years = (23 + t) years
According to question,
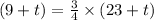
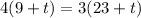
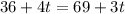
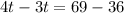
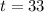
The Year in which Sue's age will be three-fourth times of Tim's age is:
= (1997 + 33) = 2030.