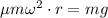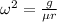Answer:2.55 rad/s
Step-by-step explanation:
Given
Diameter of ride=5 m
radius(r)=2.5 m
Static friction coefficient range=0.60-1
Here Frictional force will balance weight
And limiting frictional force is provided by Centripetal force
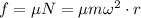
weight of object=mg
Equating two
f=mg