Question

A physics cart has a projectile launcher mounted on top. While traveling on a straight track at 0.500 m/s, a projectile is fired. It lands back in the same place on top of the launcher after the cart has moved a distance of 2.30 m. In the frame of reference of the cart, (a) at what angle was the projectile fired and (b) what was the initial velocity of the projectile? (c) What is the shape of the projectile as seen by an observer on the cart? A physics student is watching the demonstration from a classroom seat. According to the student, (d) what is the shape of the projectile’s path, and (e) what is its initial velocity?

Answer 1

(a)
`90^(\circ)`

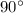
(b) Initial velocity of the projectile is 22.54 m/s

(c) Straight line perpendicular to the plane of the car's motion

(d) Parabolic

(e) The initial velocity is 23.04 m/s

Solution:

As per the question:

Velocity of the cart, v = 0.500 m/s

Distance moved by the cart, d = 2.30 m

Now,

(a) The projectile must be fired at an angle of
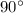`90^(\circ)` so that it mounts on the top of the cart moving with constant velocity.

(b) Now, for initial velocity, u':

Time of flight is given by;

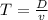`T = (D)/(v)` (1)

where

T = Flight time

D = Distance covered

(b) The component of velocity w.r.t an observer:

Horizontal component,
`v_(x) = u'cos\theta`

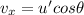
Vertical component,
`v_(y) = u'sin\theta - gT`

Also, the vertical component of velocity at maximum height is zero,
`v_(y) = 0`

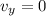
Therefore,
`T = (u')/(g)`

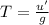
Total flight time,
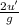`(2u')/(g)` (2)

Now, from eqn (1) and (2):

`u' = (gD)/(2v)`

`u' = (9.8* 2.30)/(2* 0.500) = 22.54 m/s`

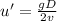
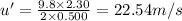
(c) The shape of the projectile w.r.t an observer will be a straight line perpendicular to the plane of cart's motion.

(d) The shape of the path of the projectile seen by the physics student outside the reference frame of the cart is parabolic

(e) The initial velocity is given by:

u = u' + v = 22.54 + 0.5 = 23.04 m/s