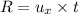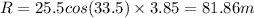Answer:
Step-by-step explanation:
Given
Initial velocity(u)=25.5 m/s
Projection angle
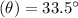
ball is 18.5 m above the ground
Time of flight for zero vertical displacement is
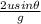
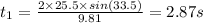
its vertical velocity will be equal to initial vertical velocity but it will be downward direction at the completion of zero vertical displacement
Now time taken to cover 18.5 m vertical displacement

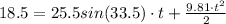

t=0.979 s
Thus
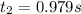
Total time to reach ground
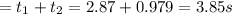
Horizontal Distance traveled in 3.85 s