Question

The base of a solid right pyramid is a regular hexagon with a radius of 2x units and an apothem of units. A solid right pyramid has a regular hexagonal base with a radius of 2 x units and an apothem of x StartRoot 3 EndRoot units. Which expression represents the area of the base of the pyramid? x squared StartRoot 3 EndRoot units2 3 x squared StartRoot 3 EndRoot units2 4 x squared StartRoot 3 EndRoot units2 6 x squared StartRoot 3 EndRoot units2

Answer 1

D

Explanation:

Answer 2

`6 x^2*√(3)`

Explanation:

The base of the pyramid we need to study is a hexagon.

Let's look at the attached image of an hexagon to understand how we are going to find the area of this figure.

Notice that an hexagon is the combination of 6 exactly equal equilateral triangles in our case of size "2x" (notice that the "radius" of the hexagon is given as "2x")

Therefore the area of the hexagon is going to be 6 times the area of one of those equilateral triangles.

We know the area of a triangle is the product of its base times its height, divided by 2:
`(base*height)/(2) = (2x*height)/(2)`

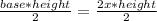
We notice that the triangle's height is exactly what is called the "apothem" of the hexagon (depicted in green in our figure) which measures
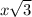`x√(3)`, so replacing this value in the formula above for the area of one of the triangles:

`(2x*height)/(2)= (2x*x√(3) )/(2)=x^2√(3)`

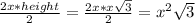
Then we multiply this area times 6 to get the total area of the hexagon (6 of these triangles):

Area of hexagon =
`6x^2√(3)`

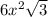
which is the last option given in the list.