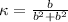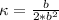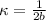Answer:
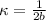
Step-by-step explanation:
The equation for kappa ( κ) is
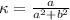
we can find the maximum of kappa for a given value of b using derivation.
As b is fixed, we can use kappa as a function of a
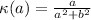
Now, the conditions to find a maximum at
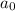 are:
are:
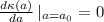
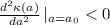
Taking the first derivative:
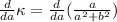
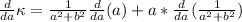
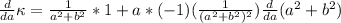
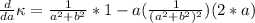
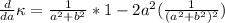
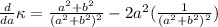
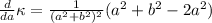
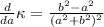
This clearly will be zero when
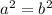
as both are greater (or equal) than zero, this implies
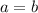
The second derivative is
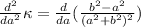
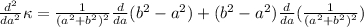
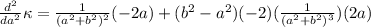
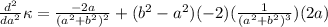
We dcan skip solving the equation noting that, if a=b, then
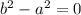
at this point, this give us only the first term
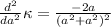
if a is greater than zero, this means that the second derivative is negative, and the point is a minimum
the value of kappa is