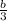Question

C=(s+b/3)m solve for s

halp

Answer 1

see explanation

Explanation:

Given

c = (s +
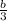`(b)/(3)`) m

There are 2 possible approaches

Approach 1

Divide both sides by m

`(c)/(m)` = s +
`(b)/(3)`

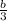
Multiply both sides by 3 to clear the fraction

`(3c)/(m)` = 3s + b ( subtract b from both sides )

`(3c)/(m)` - b = 3s ( divide both sides by 3 )

`(3c)/(3m)` -
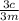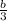`(b)/(3)` = s, cancelling the factor 3 gives

s =
`(c)/(m)` -
`(b)/(3)`

----------------------------------------------------------------------------------------

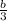
Approach 2

Distribute the right side by m

c = ms +
`(bm)/(3)`

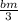
Multiply through by 3 to clear the fraction

3c = 3ms + bm ( subtract bm from both sides )

3c - bm = 3ms ( divide both sides by 3m )

`(3c)/(3m)` -
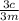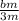`(bm)/(3m)` = s, thus

s =
`(c)/(m)` -
`(b)/(3)`