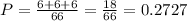Question

A student buys 2 pairs of socks at a time. He has a total of 6 pairs, 2 pairs (4 socks) of type A socks, 2 pairs of type B socks, and 2 pairs of type C socks. So he has 12 socks total, 4 of each type. The student stores the socks randomly in a basket. In the morning it is dark so the student cannot see what type of sock he is pulling from the basket. If he pulls 2 socks from the basket, what is the probability that they match?

Answer 1

The probability is 0.2727

Explanation:

There are nCk combinations or ways to take k elements from a group of n elements. So, nCk is calculated as:

`nCk=(n!)/(k!(n-k)!)`

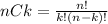
Then, there are 66 ways to select two socks from the 12 that are in the basket. This is calculated as:

`12C2=(12!)/(2!(12-2)!)=66`

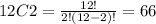
Additionally, if the student match the socks, he have 3 possibilities:

1. He match socks type A

2. He match socks type B

3. He match socks type C

There are 6 ways to match socks type A, 6 ways to match socks type B and 6 ways to match socks type C. This is calculated as:

`4C2=(4!)/(2!(4-2)!)=6`

Because the student should select 2 socks type A from the 4 socks type A that are in the basket and it is the same calculation for socks type B and Type C.

Finally, there are 18 possibilities to match the socks, so the probability is calculated as:

`P=(6+6+6)/(66)=(18)/(66)=0.2727`