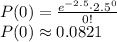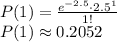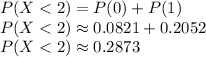1 Answer

Ask a Question

JamesGold · Answer 1 · 2020-05-06T15:14:44+0000

Answer:

The probability that 5 messages are received in 1 hour is
$P(5)\approx 0.1755$

The probability that 10 messages are received in 1.5 hours is
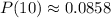
$P(10)\approx 0.0858$

The probability that less than 2 messages are received in 1/2 hour is
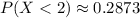
$P(X<2) \approx 0.2873$

Explanation:

The probability distribution of a Poisson random variable representing the number of successes occurring in a given time interval or a specified region of space is given by the formula:

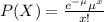$P(X)=(e^(-\mu)\mu^(x) )/(x!)$ where

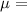$\mu =$ mean number of successes in the given time interval or region of space.

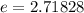
e=2.71828

a) What is the probability that 5 messages are received in 1 hour?

From the information given we know that
$\mu=5$

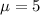
Applying the Poisson random variable formula we get:

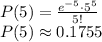
$P(5)=(e^(-5)\cdot 5^(5))/(5!)\\P(5)\approx 0.1755$

b) What is the probability that 10 messages are received in 1.5 hours?

We know from the information given that in 1 hour, 5 messages are received. In 0.5 hours we received 2.5 messages therefore in 1.5 hours we received 7.5 messages
$\mu=7.5$

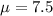
Applying the Poisson random variable formula we get:

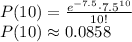
$P(10)=(e^(-7.5)\cdot 7.5^(10))/(10!)\\P(10)\approx 0.0858$

c) What is the probability that less than 2 messages are received in 1/2 hour?

We know from the information given that in 1 hour, 5 messages are received therefore in 0.5 hours we received 2.5 messages
$\mu=2.5$

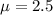
To find the probability that less than 2 messages are received in 1/2 hour we find the values when
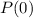P(0) and
P(1) because
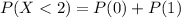
P(X<2)=P(0)+P(1)

Applying the Poisson random variable formula we get:

$P(0)=(e^(-2.5)\cdot 2.5^(0))/(0!)\\P(0)\approx 0.0821$

$P(1)=(e^(-2.5)\cdot 2.5^(1))/(1!)\\P(1)\approx 0.2052$

$P(X<2)=P(0)+P(1)\\P(X<2)\approx 0.0821+0.2052\\P(X<2) \approx 0.2873$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions