Question

A stone is thrown with an initial velocity of 30 ​ft/s from the edge of a bridge that is 43 ft above the ground. The height of this stone above the ground t seconds after it is thrown is ​f(t)equalsminus16t squaredplus30tplus43. If a second stone is thrown from the​ ground, then its height above the ground after t seconds is given by ​g(t)equalsminus16t squaredplusv0​t, where v0 is the initial velocity of the second stone. Determine the value of v0 such that the two stones reach the same high point.

Answer 1

The value of
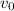`v_(0)` such that the two stones reaches the same maximum height is

`v_(0)=(√(913) )/(2) (ft)/(s)`

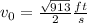
Step-by-step explanation:

For the first stone, we need to find the maximum height reached, and for that we have to derivate the given position function

`f(t)=-16t^(2)+30t+43`

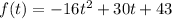
derivating, we get

`f'(t)=-32t+30`

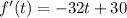
now we have to equalize the derivate to zero, and clear t

`0=-32t+30`

`t=(30)/(32)s`

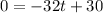
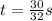
then, if we put this value of t in the position function, we obtain that the maximum height for the stone is

`f_(max)=(913)/(16)ft`

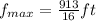
For the other stone, we have the given position function

`f(t)=-16t^(2)+v_(0)t`

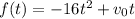
And again, derivating and clearing t, we obtain

`t=(v_(0))/(32)s`

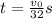
As the height must be the same for both stones, we can substitute in the position function theese values

`(913)/(16)=-16((v_(0))/(32))^(2)+v_(0)((v_(0))/(32))`

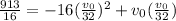
From where our value for
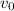`v_(0)` results to be

`v_(0)=(√(913) )/(2)(ft)/(s)`

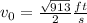
Hence, this is the value needed for the second stone to reach the same maximum height than the first stone.