Answer:
The value of
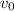 such that the two stones reaches the same maximum height is
such that the two stones reaches the same maximum height is

Step-by-step explanation:
For the first stone, we need to find the maximum height reached, and for that we have to derivate the given position function
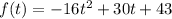
derivating, we get
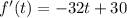
now we have to equalize the derivate to zero, and clear t
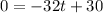

then, if we put this value of t in the position function, we obtain that the maximum height for the stone is
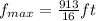
For the other stone, we have the given position function
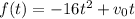
And again, derivating and clearing t, we obtain
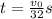
As the height must be the same for both stones, we can substitute in the position function theese values
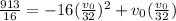
From where our value for
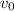 results to be
results to be

Hence, this is the value needed for the second stone to reach the same maximum height than the first stone.