Question

A ball is tossed from an upper-story window of a building. The ball is given an initial velocity of 8.00 m/s at an angle of 20.0° below the horizontal. It strikes the ground 3.00 s later. How long does it take the ball to reach a point 10.0 m below the level of launching?

Answer 1

Explanation :

When a ball is tossed from an upper storey window off a building, the height of the object as a function of time is given by :

`h(t)=ut+(1)/(2)at^2`

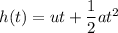
Here, u = 8 m/s

The ball strikes at an angle of 20 degrees below the horizontal. We need to find the time taken by the ball to reach a point 10 meters below the level of launching such that, h (t) = 10 m and a = g = 9.8

`10=ucos(20)t+(1)/(2)* 9.8* (t)^2`

`10=0.93* 8t+4.9t^2`

`10=7.51t+4.9t^2`

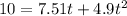
After solving the above equation, t = 0.855 seconds

So, the ball will take 0.855 seconds to reach a point 10 m below the level of launching. Hence, this is the required solution.