Question

Suppose you invest $ 1 comma 100 in an account paying 8 % interest per year. a. What is the balance in the account after 4 ​years? How much of this balance corresponds to​ "interest on​ interest"? b. What is the balance in the account after 27 ​years? How much of this balance corresponds to​ "interest on​ interest"? a. What is the balance in the account after 4 ​years? The balance in the account after 4 years is ​$ 1496.54 1496.54. ​(Round to the nearest​ cent.) How much of this balance corresponds to​ "interest on​ interest"? The amount that corresponds to interest on interest is ​$ nothing. ​(Round to the nearest​ cent.) b. What is the balance in the account after 27 ​years? The balance in the account after 27 years is ​$ nothing. ​(Round to the nearest​ cent.) How much of this balance corresponds to​ "interest on​ interest"? The amount that corresponds to interest on interest is ​$ nothing. ​(Round to the nearest​ cent.)

Answer 1

when time = 4 years:

Amount 1,360.49

"the interest on interest" 40.49

when time = 27 years:

Amount 7,988.06

"the interest on interest" 4,828,06

Step-by-step explanation:

we calcualte the future balance usign the compound interest formula:

`Principal \: (1+ r)^(time) = Amount`

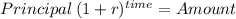
Principal 1,000.00

time 4.00

rate 0.08000

`1000 \: (1+ 0.08)^(4) = Amount`

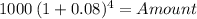
Amount 1,360.49

"the interest on interest" will be the compounding.

It will be the difference betwene simple interest and compounding:

1,000 x (1+0.08x4) = 1,000 x 1.32 = 1,320

1,360.49 - 1,320 = 49.49

if time 27.00

`1000 \: (1+ 0.08)^(27) = Amount`

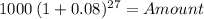
Amount 7,988.06

interest on interest:

1,000 x (1+0.08x27) = 1,000 x 3.16 = 3,160

7,988.06 - 3,160 =