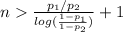Answer:
a) You do not have enough to decide the coin is fake
b) You should choose n as the least positive integer such that
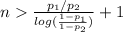
Explanation:
a)
If the coin is fair, the probability of head = probability of tail = 0.5 .
If the event of tossing the coin follows the Bernoulli's distribution (also called binomial distribution), then the probability of 1 head in four tosses is
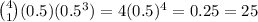
Since this probability is much less than 50%, it is too early to decide that the coin is not fair.
b)
Suppose you perform the experiment n times in the two scenarios. The probability of having 1 success and n-1 failures in scenario 1 would be
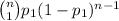
whereas in scenario 2 would be
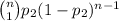
Obviously, you would select scenario 1 if
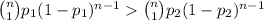
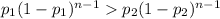

Since the function log(x) is increasing, we can take log on both sides to get

Since
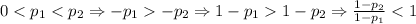
and
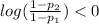
Therefore
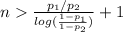
So, you should choose n as the least positive integer such that