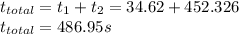Question

A boat moves through the water of a river at 4.72 m/s relative to the water, regardless of the boat’s direction. If the current is flowing at 3.86 m/s, how long does it take the boat to complete a trip consisting of a 297 m displacement downstream followed by a 389 m displacement upstream? Answer in units of s.

Answer 1

486.95s

Step-by-step explanation:

Let the velocity of the boat be
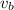`v_b` and that of the river be
`v_r`.

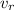When the boat is moving downstream, the resultant velocity is given by;

`v=v_b+v_r\\Given;\\v_b=4.72m/s\\v_r=3.86m/s\\therefore\\v=4.72m/s+3.86m/s=8.58m/s`

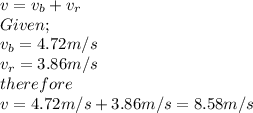
Recall that

`velocity=(dispacement)/(time).............(1)`

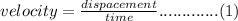
Given; downstream displacement, d = 297m. Therefore by equation (1);

`8.58=(297)/(t_1)\\t_1=(297)/(8.58)\\t_1=34.62s`

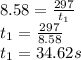
where
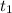`t_1` is the time taken to travel downstream displacement.

When the boat is moving upstream it is moving directly against the river current, hence its resultant velocity in this case becomes;

`v=v_b-v_r\\v=4.72-3.86=0.86m/s`

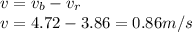
The time taken upstream is then calculated as follows given that the upstream displacement is 389m, according to equation (1);

`0.86=(389)/(t_2)\\`

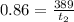
therefore
`t_2=(389)/(0.86)=452.326s`

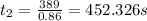
Hence the total time taken by the boat to complete its trip as specified is given as follows;

`t_(total)=t_1+t_2= 34.62+452.326\\t_(total)=486.95s`

Answer 2

Total time taken by boat to cover all the displacement = 452.3254 sec

Step-by-step explanation:

We have given speed of boat = 4.72 m/sec

Speed of current flowing = 3.86 m./sec

In downstream relative speed of boat = speed of boat + speed of current flowing = 4.72+3.86 = 8.58 m/sec

Distance traveled downstream = 297 m

So time taken by boat to travel 297 m downstream
`t_1=(297)/(8.58)=34.615sec`

In upstream relative speed of speed = speed of boat - speed of current flowing = 4.72 -3.86 = 0.86 m/sec

Distance traveled in upstream = 389 m

So time taken to travel 289 m upstream
`t_2=(389)/(0.86)=452.325sec`

So total time
`t=t_1+t_2=34.615+452.325486.94 sec`