Answer:
The space station must turn at 0.24 rad/s to give the astronauts inside it apparent weights equal to their real weights at the earth’s surface.
Step-by-step explanation:
In circular motion there’s always a radial acceleration that points toward the center of the circumference, so because the space station is spinning like a centrifuge it has a radial acceleration towards the center of the trajectory. To imitate the weight of the passengers on earth, they should turn the station in a way that the radial acceleration equals earth gravitational acceleration; this is:
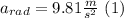
And radial acceleration is also defined as:
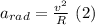
with v the tangential velocity of the station and R the radius of the ring, solving for v:
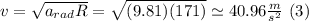
We can find the angular velocity using the following equation:
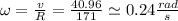
That is the angular velocity the space station must turn.