Answer:
False
Explanation:
Lets call the three prime divisors of n p, q, and r, being r the largest, we know:
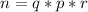
Now, if
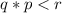
then
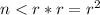
So:

Also, for every natural greater than one, we know:
![\sqrt[3]{n}<√(n)](https://img.qammunity.org/2020/formulas/mathematics/high-school/xac126qrf100w4itrnncrh6vm2qvv1ev0f.png)
so
![\sqrt[3]{n}<√(n) < r](https://img.qammunity.org/2020/formulas/mathematics/high-school/199gxhqpx3hg8eo8z9lnmuolpwtvdj52wb.png)
from which:
![\sqrt[3]{n} < r](https://img.qammunity.org/2020/formulas/mathematics/high-school/j3xtq1kec1r9iyg84u57fo31zjxchr8hqw.png)
So, we see, this means the preposition is false, we can find a particular counterexample:
q=2
p=3
p*q = 6
We need to choose a prime greater than 6
r=7
n= 2 * 3 *7 = 42
![\sqrt[3]{42} = 3.4760 < 7](https://img.qammunity.org/2020/formulas/mathematics/high-school/hqjg9ixrpufqss7msgzw3eoem6b9m1enmu.png)