Answer:
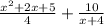
OR

Explanation:
PART A:
At the bottom, the x can be interpreted as
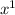 and when dividing exponents, you subtract them, so every exponent at the top will be losing a value. ((Also, I forgot to put it, but, x^2 should also be /4 ----> x^2/4
and when dividing exponents, you subtract them, so every exponent at the top will be losing a value. ((Also, I forgot to put it, but, x^2 should also be /4 ----> x^2/4
You can actually also simplify the numbers (that are divisible by 4) but the equation will look a bit different.
PART B: Basically, you are undoing everything you just did...
Remember that multiplying exponents is the equivalent of adding numbers.