Answer:
There are
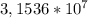 seconds in a year.
seconds in a year.
The fractional error in assuming
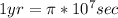 is
is
 .
.
Explanation:
Assuming a year of 365 days (non leap-years), we can found how many seconds are in a year by multiplying seconds in a minute, minutes in an hour, hours in a day and finally days in a year.
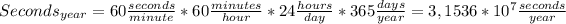
Knowing how many seconds are in a year, we can find the absolute error of the estimation by taking the module of the difference between real value and estimation:
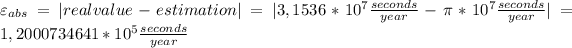
Now that we know the absolute error, we calculate the fractional error by dividing it by the real value:
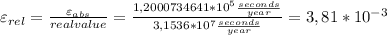
That is a minimal error, close to 0,4% and enough for every day estimations.