Answer:
If
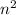 is even, then so is n.
is even, then so is n.
Explanation:
We will prove the above theorem with the help of contrapositivty.
The contrapositive statement for given statement is, if n is odd then,
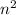 is odd. Now, all we need to prove is for odd n we have odd
is odd. Now, all we need to prove is for odd n we have odd
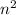 .
.
Let n be odd, then it can be written in the form
 , where t is an integer,
, where t is an integer,
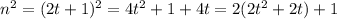
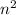 is odd as it can be expressed in the form
is odd as it can be expressed in the form
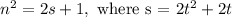 .
.
Hence, by contrapositivity, it can be said that if a number is even, then so is its square root.
But the given statement is true for
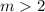 .
.