Question

Kerosene flows through 3/4 standard type K drawn copper tube. The pressure drop measured at two points 50 m apart is 130 kPa. Determine the flow rate of the kerosene

Answer 1

`Q=4.98* 10^(-3)\ m^3/s`.

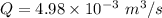Step-by-step explanation:

Given that

L= 50 m

Pressure drop = 130 KPa

copper tube is 3/4 standard type K drawn tube.

From standard chart ,the dimension of 3/4 standard type K copper tube given as

Outside diameter=22.22 mm

Inside diameter=18.92 mm

Dynamic viscosity for kerosene

`\mu =0.00164\ Pa.s`

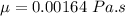
We know that

`\Delta P=(128\mu QL)/(\pi d_i^4)`

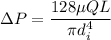
Where Q is volume flow rate

L is length of tube

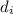`d_i` is inner diameter of tube

ΔP is pressure drop

μ is dynamic viscosity

Now by putting the values

`\Delta P=(128\mu QL)/(\pi d_i^4)`

`130* 1000=(128* 0.00164* 50Q)/(\pi * 0.01892^4)`

`Q=4.98* 10^(-3)\ m^3/s`

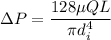
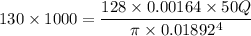
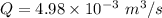
So flow rate is
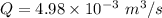`Q=4.98* 10^(-3)\ m^3/s`.