Question

Turpentine flows through a 12-nominal schedule 40 pipe. What is the flow rate that corresponds to a Reynolds number of 2000?

Answer 1

flow rate is 8.0385 ×
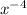`x^(-4)` m³/s or 12.741 gpm

Step-by-step explanation:

given data

12-nominal schedule 40 pipe

Reynolds number = 2000

to find out

What is the flow rate

solution

we know the diameter of 12-nominal schedule 40 pipe is

Diameter = 12.75 inch

D = 0.32385 m

and

dynamic viscosity of Turpentine is = 0.001375 Pa-s

and Density of Turpentine is 870 kg/m³

so

Reynolds number is express as

Re =
`(\rho*V*D)/(\mu)`

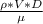
here ρ is density and D is diameter and V is velocity and µ is viscosity

so put here all value

2000 =
`(870*V*0.3238)/(0.001375)`

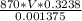
V = 9.7619 ×
`x^(-3)` m/s

and

flow rate is

Q = V × A

here A is area and Q is flow rate

Q = 9.7619 ×
`x^(-3)` ×
`(\pi )/(4) * 0.3238^2`

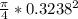
Q = 8.0385 ×
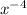`x^(-4)` m³/s

so flow rate is 8.0385 ×
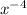`x^(-4)` m³/s or 12.741 gpm