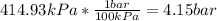Question

What is the pressure at the bottom of a 32m high water tower in gage pressure and absolute pressure (answers in kPa, and bar)

Answer 1

`P_(g)=313.6kPa, P_(g)=3.13bar, P_(a)=414.93kPa, P_(a)=4.15bar`

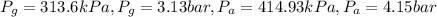
Step-by-step explanation:

The gauge pressure is the one made by the water over the bottom of the tank without taking into account the pressure of the atmosphere. It can be calculated by using the following equation:

`P_(g)=\gamma _{H_(2)O} h`

in this case:

`\gamma _{H_(2)O}=9.8kN/m^(3)`

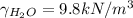
and h=32m

so the equation would then solve to:

`P_(g)=(9.8kN(m^(3))(32m)`

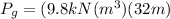
Which yields

`P_(g)=313.6kPa`

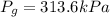
now, in order to find the bars, we must remember that:

1bar=100kPa, so

`313.6kPa*(1bar)/(100kPa)=3.136bar`

Now, in order to find the absolute pressure we need to add the atmospheric pressur to the pressures previously found.

`P_(a)=313.6kPa+101.325kPa`

`P_(a)=414.93kPa`

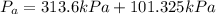
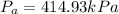
and likewise we can do the conversion of kPa to bars, so we get:

`414.93kPa*(1bar)/(100kPa)=4.15bar`