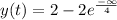Answer:
At steady state output will be 2
Step-by-step explanation:
We have given transfer function

Input is unit step so
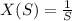
We know that
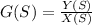 , here
, here
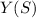 , is output
, is output
So output
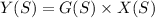
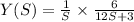
Taking 12 common from denominator
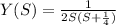
Now using partial fraction
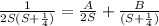
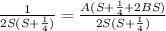
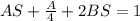
On comparing coefficient A=4 and B = -2
Putting the values of A and B in Y(S)
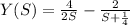
Now taking inverse la place
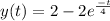
Steady state means t tends to infinite
So output at steady state =