Answer:
The measure of the largest angle is 120°
Explanation:
Lets explain how to find the measure of an angle from the length of the
sides of the triangle
- We can do that by using the cosine rule
- If the three angles of the triangle are A , B , C, then the side opposite
to angle A is BC , the side opposite to angle B is AC and the side
opposite to angle C is AB, So to find measure of angle A use the rule
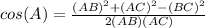
Lets solve the problem
- Assume that the triangle is ABC where AB = 14 cm , BC = 10 cm and
AC = 6 cm
- We need to find the measure of the largest angle
- The largest angle is opposite to the longest side
∵ The longest side is AB
∴ The largest angle is C
By using the rule above
∴
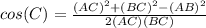
∵ AB = 14 cm , BC = 10 cm , AC = 6 cm
∴
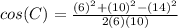
∴
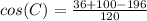
∴
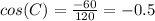
∴ cos(C) = -0.5 ⇒ that means angle C is obtuse angle
∴ m∠C =
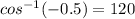
* The measure of the largest angle is 120°