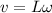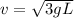Question

A thin stick is held vertically with one end on the floor and is then allowed to fall. Find the speed of the other end when it hits the floor, assuming that the end on the floor does not slip.

Answer 1

`v = √(3gL)`

Step-by-step explanation:

As we know that length of the rod is L and mass is M

so here it one end of the rod is stationary and other end of the rod is rotating about one end

then we will have energy conservation to find the total rotational kinetic energy of rod about its one end is given as

`mg(L)/(2) = (1)/(2)I\omega^2`

`mg(L)/(2) = (1)/(2)((mL^2)/(3))\omega^2`

`g = (L)/(3) \omega^2`

`\omega = \sqrt{(3g)/(L)}`

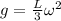
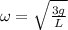
so the linear speed of the other end of the rod just before it hit the ground is given as

`v = L\omega`

`v = √(3gL)`