Answer:
total work is 99.138 kJ
Step-by-step explanation:
given data
diameter = 5 cm
depth = 75 m
density = 1830 kg/m³
to find out
the total work
solution
we know mass of volume is
volume =
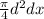
volume =
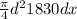
so
work required to rise the mass to the height of x m
dw =
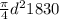 gx dx
gx dx
so total work is integrate it with 0 to 75
w =
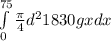
w =
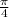 × 0.05² × 1830× 9.81×
× 0.05² × 1830× 9.81×
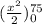
w = 99138.53 J
so total work is 99.138 kJ