Answer:
Explanation:
Given two parametric equations
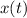 and
and
 , the first derivative can be found using the following equation:
, the first derivative can be found using the following equation:
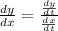
In this problem,
 and
and
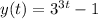 . Finding the derivative of each of these functions with respect to
. Finding the derivative of each of these functions with respect to
 gives us the following:
gives us the following:
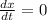
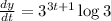
Because
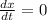 , that means the function is a vertical line and has an infinite first derivative.
, that means the function is a vertical line and has an infinite first derivative.