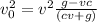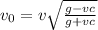Question

A particle m is thrown vertically upward with an initial velocity v. Assuming a resisting medium proportional to the velocity, where the proportionality factor is c, calculate the velocity with which the particle will strike the ground upon its return if there is a uniform gravitational field.

Answer 1

Answer:
`v_0=v\sqrt{(g-vc)/(g+vc)}`

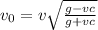
Step-by-step explanation:

Given

v=initial velocity

resisting acceleration =cv

also gravity is opposing the upward motion

Therefore distance traveled during upward motion

`v^2_f-v^2=2as`

Where a=cv+g

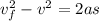
`0-v^2=2(cv+g)s`

`s=(v^2)/(2(cv+g))`

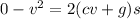
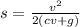
Now let v_0 be the velocity at the ground

`v^2_0-0=2(g-vc)s`

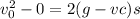
substituting s value

`v^2_0=v^2(g-vc)/((cv+g))`

`v_0=v\sqrt{(g-vc)/(g+vc)}`