Question

The height of a door is measured by four people and their measured values are 217.6 cm, 217.2 cm, 216.8 cm, and 217.9 cm. (a) What is the average value of these four measurements? (Enter your answer to the nearest tenths place.)

(b) What is the standard deviation for the four measurements?

Answer 1

The average value of the four door height measurements is 217.4 cm, and the standard deviation of these measurements is approximately 0.4 cm.

Step-by-step explanation:

To find the average value of the four measurements: 217.6 cm, 217.2 cm, 216.8 cm, and 217.9 cm, you add them up and then divide by the number of measurements, which is four:

Average = (217.6 + 217.2 + 216.8 + 217.9) / 4 = 217.375

Rounded to the nearest tenths place, the average is 217.4 cm.

For the standard deviation, we first calculate the variance. First, find the difference of each measurement from the mean, square that difference, and then find the average of those squared differences. Finally, take the square root of that average to find the standard deviation:

1. 
   
3. Sum of squared differences = (217.6 - 217.375)² + (217.2 - 217.375)² + (216.8 - 217.375)² + (217.9 - 217.375)²
4. 
   
6. Variance = Sum of squared differences / 3 (Note: Divisor is 3 because for the sample standard deviation, we use n-1)
7. 
   
9. Standard Deviation = √Variance

Substituting the values and performing the calculations gives us a standard deviation of approximately 0.4 cm.

Answer 2

a) To the nearest tenth the average value of the measures is 217.4cm

b) The standard deviation for the four measurements is 0.415

Step-by-step explanation:

The average is the result of adding all the values and dividing by the number of measures, in this case 4 then

`Average = (217.6 + 217.2 + 216.8 + 217.9)/(4) \\`

`Average = (869.5)/(4) \\`

`Average = 217.375`

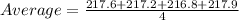
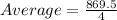
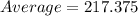
a) To the nearest tenth the average value of the measures is 217.4cm

The standard deviation equals to the square root of the variance, and the variance is the adition of all the square of the difference between the measure and the average for each value divided by the number of measurements

So first, we must calculate the variance:

`Variance = ((217.6-217.4)^2+(217.2-217.4)^2+(216.8-217.4)^2+(217.9-217.4)^2)/(4)`.

`Variance = ((0.2)^2+(-0.2)^2+(-0,6)^2+(0.5)^2)/(4)`.

`Variance = (0.04+0.04+0.36+0.25)/(4)`.

`Variance = (0.69)/(4)`.

`Variance = 0.1725`.

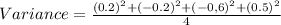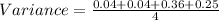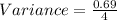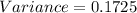This represent the difference between the average and the measurements.

Now calculate the standard deviation

Standard deviation =
`√(Variance)`

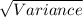
Standard deviation =
`√(0.1725)`

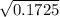
Standard deviation = 0.415

b) The standard deviation for the four measurements is 0.415

This measure represent a standard way to know what is normal in this sample. so the differences between the average should be of ±0.415