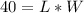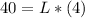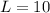Answer:
Explanation:
From the problem statement, we can set up the following two equations:
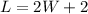
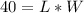
Plugging the first equation into the second, we can solve for
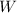 :
:
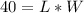
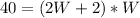
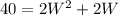
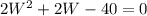
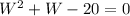
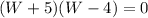
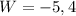
Since the length must be a positive number, then we know that
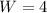 . We can now plug this number into the second equation to get
. We can now plug this number into the second equation to get
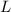 :
: