Answer:
Distance covered by the train, x = 493.72 meters
Step-by-step explanation:
It is given that,
Initial speed of the train, u = 80 km/h = 22.22 m/s
Final speed of the train, v = 0 (it stops)
Acceleration of the train,
 (it decelerates)
(it decelerates)
Let x is the distance the train travels from the time the conductor applies the brakes until the train comes to a complete stop. It can be calculated using the kinematic formula as :

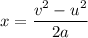
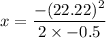
x = 493.72 meters
So, the distance covered by the train from the time the conductor applies the brakes until the train comes to a complete stop is 493.72 meters. Hence, this is the required solution.