Question

An archeologist has found a fossilized leg bone of some unknown mammal. Based on the size of the bone, she determines that it should have contained about 100 g of carbon-14 when the animal was alive. Knowing that the half-life of carbon-14 is 5730 years, write an equation that will model how much carbon-14 is left in the bone now after "t" years.

Answer 1

Therefore, required equation is N = 100 x
`2^{- (t)/(5730 )`

Explanation:

According to the question it is given that

Amount of carbon atom when animal was alive is
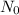`N_0` = 100g

Half life of C-14 is 5730 years

Let 'N' be the amount of carbon atom present after 't' time

since the differential equation of decay process of radioactive atom is

`(dN)/(dt) = \lambda N` where, λ is the decay constant

on solving this we get

`N = N_0 e^(-\lambda t)`

on further solving and substituting
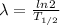`\lambda = (ln2)/(T_(1/2))` we get

`N = N_0 2^{- (t)/(T_(1/2)) }`

on substituting the value of
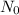`N_0` = 100g and
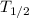`T_(1/2)` = 5730 we get

N = 100 x
`2^{- (t)/(5730 )`