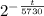Answer:
Therefore, required equation is N = 100 x
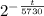
Explanation:
According to the question it is given that
Amount of carbon atom when animal was alive is
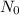 = 100g
= 100g
Half life of C-14 is 5730 years
Let 'N' be the amount of carbon atom present after 't' time
since the differential equation of decay process of radioactive atom is
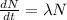 where, λ is the decay constant
where, λ is the decay constant
on solving this we get
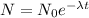
on further solving and substituting
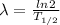 we get
we get
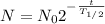
on substituting the value of
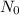 = 100g and
= 100g and
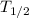 = 5730 we get
= 5730 we get
N = 100 x