Question

A car on a straight flat road races a boat on calm canal parallel to the road. The car has a constant acceleration of 1.95 m/ s2 and reaches a top speed of 41.0 m/s. The boat has a constant acceleration of 6.50 m/ s2 and reaches a top speed of 32.0 m/s. The car and the boat accelerate to their top speeds and then maintain their top speeds for the remainder of the race. They race for 1.20 km. Determine which vehicle wins the race.

Answer 1

Step-by-step explanation:

There are 3 equations to use.

The velocity v for a given constant acceleration a in a time t:

(1)
`v = at`

The distance x traveled with a constant acceleration a in a given time t:

(2)
`x=(1)/(2)at^2`

The distance x traveled for a constant velocity v in a time t:

(3)
`x=vt`

To calculate the time t during the acceleration phase use equation 1:

`t=(v)/(a)`

`t_(car)=21 s`

`t_(boat)=4.9 s`

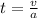
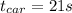
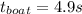
For the distance traveled during the acceleration use equation 2:

`x_(car)=431m\\x_(boat)=78.8m`

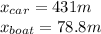
Use equation 3 to calculate the time t for the remaining distance:

`t=(1200-x)/(v)`

`t_(car)=18.8s\\t_(boat)=35s`

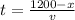
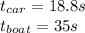
Add up the times for the car and the boat:

`t_(car)=39.8s\\t_(boat)=39.9s`

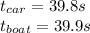
The car wins.