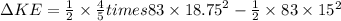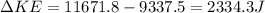Question

An object, with mass 83 kg and speed 15 m/s relative to an observer, explodes into two pieces, one 4 times as massive as the other; the explosion takes place in deep space. The less massive piece stops relative to the observer. How much kinetic energy is added to the system during the explosion, as measured in the observer's reference frame

Answer 1

The amount of Kinetic energy added to the system is 2334.3J

Solution:

As per the question:

Mass of object, m = 83 kg

Relative velocity of the object,
`v_(mb) = v_(m) - v_(o) = 15 m/s`

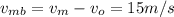
After the explosion,

mass of the fragment is M and the other fragment, M' = 4M

Velocity of the lighter fragment after collision, v = 0 m/s

Now,

Mass of heavier fragment, M' =
`(4)/(5)m`

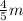
Mass of lighter fragment, M' =
`(1)/(5)m`

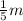
Let the velocity of the heavier fragment be v'.

Therefore by the law of conservation of momentum, we have:

Momentum of the object before collision = Momentum of the object after collision

`mv_(mo) = Mv + M'v'`

`mv_(mo) = M.0 + (4)/(5)mv'`

`v' = (5)/(4)* 15 = 18.75 m/s`

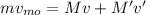
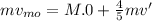
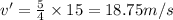
Now, the change in Kinetic Energy gives the amount of Kinetic energy added to the system:

`\Delta KE = KE_(final) - KE_(initial)`

`\Delta KE = (1)/(2)Mv'^(2) - (1)/(2)mv_(mo)^(2)`

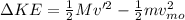
Since, the lighter particle stops, it won't have any kinetic energy.

`\Delta KE = (1)/(2)* (4)/(5)times 83* {18.75}^(2) - (1)/(2)* 83* 15^(2)`

`\Delta KE = 11671.8 - 9337.5 = 2334.3 J`