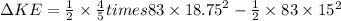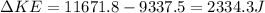Answer:
The amount of Kinetic energy added to the system is 2334.3J
Solution:
As per the question:
Mass of object, m = 83 kg
Relative velocity of the object,
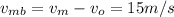
After the explosion,
mass of the fragment is M and the other fragment, M' = 4M
Velocity of the lighter fragment after collision, v = 0 m/s
Now,
Mass of heavier fragment, M' =
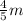
Mass of lighter fragment, M' =
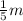
Let the velocity of the heavier fragment be v'.
Therefore by the law of conservation of momentum, we have:
Momentum of the object before collision = Momentum of the object after collision
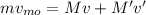
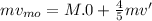
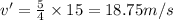
Now, the change in Kinetic Energy gives the amount of Kinetic energy added to the system:
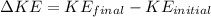
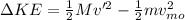
Since, the lighter particle stops, it won't have any kinetic energy.