Question

A speedboat starts from rest and accelerates at - 2.01 m/s2 for 7.00 s. At the end of this time, the boat continues for an additional 6.00 s with an acceleration of +0.518 Following this, the boat accelerates at 1.49 m/s2 for 8.00 s (a) What is the velocity of the boat at t = 21.0 s? (b) Find the total displacement of the boat.

Answer 1

(a) 52.724 m/s

(b) Total displacement, d = 551.25 m

Solution:

As per the question:

Initial acceleration of the speed boat, a = - 2.01
`m/s^(2)`

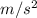
Time duration, t = 7.00 s

Additional time, t' =6.00 s

Acceleration for additional time, a' = 0.518
`m/s^(2)`

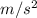
The followed up acceleration, a'' = 1.49
`m/s^(2)`

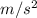
Time duration, t'' = 8.00 s

(a) Now, to calculate the velocity of the boat at timer, t = 21.0 s, we have:

After the initial 7.00 s, the velocity of the boat, from eqn-1 of motion:

v = u + at

v = 0 - 2.1(7.00) = - 14.7 m/s

After t + t' = 13 s:

v' = v + at

v' = 14.7 + 0.518(13) = 21.434 m/s

Now, velocity of the boat after t = 21 s:

v'' = v' + a''t

v'' = 21.434 + 1.49(21) = 52.724 m/s

(b) Now, the total displacement, d:

For the first case:

d = ut +
`(1)/(2)at^(2) = 0 - 0.5* 2.1* 7^(2) = - 51.45 m`

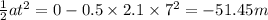
For the second case:

d = v't' = 21.434(6) = 128.6 m

For the third case:

d = ut +
`(1)/(2)a't'^(2) = 0 + 0.5* 0.518* 6^(2) = 4.65 m`

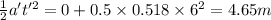
For the fourth case:

d = v''t'' = 52.724(8) = 421.79 m

For the last case:

d = ut +
`(1)/(2)a't'^(2) = 0 + 0.5* 1.49* 8^(2) = 47.68 m`

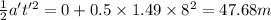
Total displacement, d = -51.45 + 128.6 + 4.65 + 421.79 + 47.68 = 551.25 m