Question

8. Suppose that the demand for bentonite is given by Q = 40 − 0.5P, where Q is in tons of bentonite per day and P is the price per ton. Bentonite is produced by a monopolist at a constant marginal and average total cost of $10 per ton. How much profit is earned per day if the profit-maximizing quantity of bentonite is sold at the profit-maximizing price?

Answer 1

The total profit is 612.5

Step-by-step explanation:

First we need to find the profit maximizing quantity. Since the monopolist faces the entire demand his profit (
`\Pi`)equation would be

`\Pi=Q* P- 10 Q`

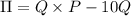
where PxQ is his revenue and 10Q is his total cost.

We can replace P in the above equation from the equation demand
`Q=40-(P)/(2)\rightarrow P=80-2Q`

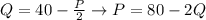
Then

`\Pi=Q* (80-2Q)- 10 Q=80Q-2Q^2-10Q`

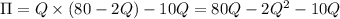
taking derivatives with respect to Q

`(\partial \Pi)/(\partial Q)=80-4Q-10=0`

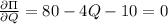
then Q=17.5 and P=45.

The total profit is then 612.5