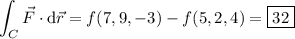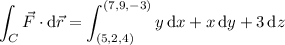
Parameterize the line segment (call it
 ) by
) by
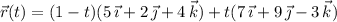
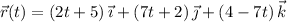
with
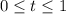 . Then
. Then

and the line integral is
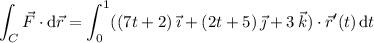
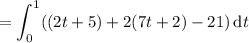

Alternatively, if we can show that
 is conservative, then we can apply the fundamental theorem of calculus. We need to find
is conservative, then we can apply the fundamental theorem of calculus. We need to find
 such that
such that
 , which requires
, which requires
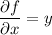
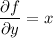
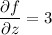
Integrating both sides of the first equation with respect to
 gives
gives
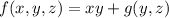
Differentiating both sides wrt
 gives
gives
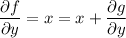
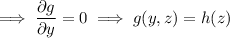
Differentiating wrt
 gives
gives

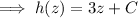
So we have

and
 is conservative. By the FTC, we find
is conservative. By the FTC, we find