Question

(CO 3) On average, the parts from a supplier have a mean of 97.5 inches and a standard deviation of 6.1 inches. Find the probability that a randomly selected part from this supplier will have a value between 87.5 and 107.5 inches. Is this consistent with the Empirical Rule of 68%-95%-99.7%? Probability is 0.90, which is consistent with the Empirical Rule Probability is 0.95, which is inconsistent with the Empirical Rule Probability is 0.90, which is inconsistent with the Empirical Rule Probability is 0.05, which is consistent with the Empirical Rule Flag this Question

Answer 1

C. Probability is 0.90, which is inconsistent with the Empirical Rule.

Explanation:

We have been given that on average, the parts from a supplier have a mean of 97.5 inches and a standard deviation of 6.1 inches.

First of all, we will find z-score corresponding to 87.5 and 107.5 respectively as:

`z=(x-\mu)/(\sigma)`

`z=(87.5-97.5)/(6.1)`

`z=(-10)/(6.1)`

`z=-1.6393`

`z\approx-1.64`

`z=(x-\mu)/(\sigma)`

`z=(107.5-97.5)/(6.1)`

`z=(10)/(6.1)`

`z=1.6393`

`z\approx 1.64`

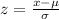
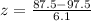
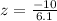
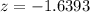
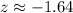
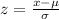
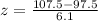
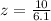
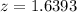
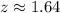
Now, we need to find the probability
`P(-1.64<z<1.64)`.

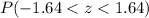Using property
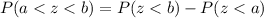`P(a<z<b)=P(z<b)-P(z<a)`, we will get:

`P(-1.64<z<1.64)=P(z<1.64)-P(z<-1.64)`

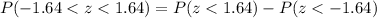
From normal distribution table, we will get:

`P(-1.64<z<1.64)=0.94950-0.05050`

`P(-1.64<z<1.64)=0.899`

`P(-1.64<z<1.64)\approx 0.90`

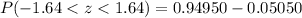
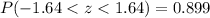
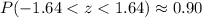
Since the probability is 0.90, which is inconsistent with the Empirical Rule, therefore, option C is the correct choice.