Answer: FIRST OPTION.
Explanation:
By definition, the "Angle formed by a Tangent and a Secant" is:
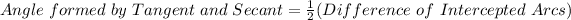
In this case you can identify in the figure that the Intercepted Arcs are:
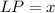 and
and
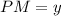
And the Angle formed by the tangent and the secant is:

Therefore, the following equation can be used to calculate the measure of the angle ∠MNP:

This matches with the First option.