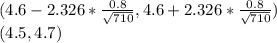Question

A marketing research company desires to know the mean consumption of milk per week among males over age 32. A sample of 710 males over age 32 was drawn and the mean milk consumption was 4.6 liters. Assume that the population standard deviation is known to be 0.8 liters. Construct the 98% confidence interval for the mean consumption of milk among males over age 32. Round your answers to one decimal place.

Answer 1

(4.5, 4.7)

Explanation:

Hi!

Lets call X to the consumption of milk per week among males over age 32. X has a normal distribution with mean μ and standard deviation σ.

`X \sim N(\mu, \sigma)`

When you know the population standard deviation σ of X , and the sample mean is
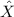`\hat X`, the variable q has distribution N(0,1):

`q = (\hat X - \mu)/(\sigma) \sim N(0,1)`

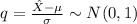
Then you have:

`P(-k < q <k ) = P(\hat X -(\sigma)/(√(N) )<\mu<\hat X +(\sigma)/(√(N) ))=C`

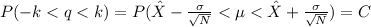
This defines a C - level confidence interval. For each C the value of k is well known. In this case C = 0.98, then k = 2.326

Then the confidence interval is:

`(4.6 - 2.326*(0.8)/(√(710)), 4.6 + 2.326*(0.8)/(√(710)))\\ (4.5, 4.7)`