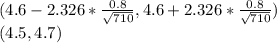Answer:
(4.5, 4.7)
Explanation:
Hi!
Lets call X to the consumption of milk per week among males over age 32. X has a normal distribution with mean μ and standard deviation σ.
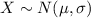
When you know the population standard deviation σ of X , and the sample mean is
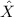 , the variable q has distribution N(0,1):
, the variable q has distribution N(0,1):
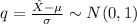
Then you have:
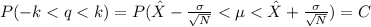
This defines a C - level confidence interval. For each C the value of k is well known. In this case C = 0.98, then k = 2.326
Then the confidence interval is: