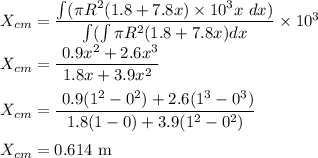Question

A light hollow tube of 2.00 cm diameter and 1.0 m length is filled with tiny beads of different density. The resulting density distribution is linear, with the left end having a density of 1.8 g/cm3, and the right end having a density of 9.6 g/cm3. How far from the left end will be the center of mass (give answer in cm)?

Answer 1

The centre of mass will be at a distance of 0.614 m from the left end of the light hollow tube.

Answer 2

The centre of mass will be at a distance of 0.614 m from the left end of the light hollow tube.

Step-by-step explanation:

Given:

Diameter of the hollow pipe= 2 cm

Length of the hollow tube=1 m

Density at the left
`=1.8*10^3\ kg/ m^3`

Density at the right end
`=9.6* 10^3 kg/ m^3`

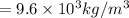
Let the density of the tube varies as

`\rho=a+bx`

putting the end points of density as follows we have

`1.8*10^3=a+b*0`

`9.6*10^3=a+b* 1`

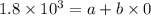
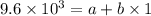
we get a=1.8
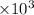`*10^3` and
`b=7.8*10^3`

`\rho=(1.8+7.8x)* 10^3`

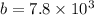
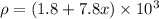
where

• a and b are constants.
• x is the distance from left end.

We know that the x coordinate centre of the mass is given by

`X_(cm)=(\int dm\ x)/(\int dm)`

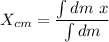
where dm is the mass of an element given by

`dm=\pi R^2(1.8+7.8x)* 10^3dx`

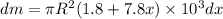
Now we have

`X_(cm)=(\int (\pi R^2(1.8+7.8x)*10^3x\ dx))/(\int (\int \pi R^2(1.8+7.8x) dx)* 10^3\\X_(cm)=(\ 0.9x^2+2.6x^3)/(1.8x+3.9x^2)\\\\X_(cm)=(\ 0.9(1^2-0^2)+2.6(1^3-0^3))/(1.8(1-0)+3.9(1^2-0^2))\\\\X_(cm)=0.614\ \rm m`