Answer:
Step-by-step explanation:
For an object to move with constant velocity, the acceleration of the object must be zero:
 .
.
As the net force equals acceleration multiplied by mass , this must mean:
 .
.
So, the sum of the three forces must be zero:
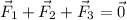 ,
,
this implies:
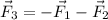 .
.
To obtain this sum, its easier to work in Cartesian representation.
First we need to define an Frame of reference. Lets put the x axis unit vector
 pointing east, with the y axis unit vector
pointing east, with the y axis unit vector
 pointing south, so the positive angle is south of east. For this, we got for the first force:
pointing south, so the positive angle is south of east. For this, we got for the first force:
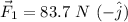 ,
,
as is pointing north, and for the second force:
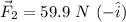 ,
,
as is pointing west.
Now, our third force will be:
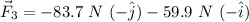
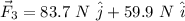
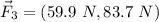
But, we need the magnitude and the direction.
To find the magnitude, we can use the Pythagorean theorem.
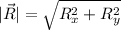
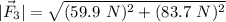
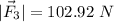
this is the magnitude.
To find the direction, we can use:

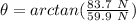
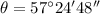
and this is the angle south of east.