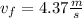Question

Object A is moving due east, while object B is moving due north. They collide and stick together in a completely inelastic collision. Momentum is conserved. Object A has a mass of mA = 18.5 kg and an initial velocity of v0A = 8.15 m/s, due east. Object B, however, has a mass of mB = 30.5 kg and an initial velocity of v0B = 5.00 m/s, due north. Find the magnitude of the final velocity of the two-object system after the collision.

Answer 1

The magnitude of the final velocity of the two-object system is
`v=4.37(m)/(s)`

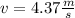
Step-by-step explanation:

As the Momentum is conserved, we can compare the instant before the collision, and the instant after. Also, we have to take in account the two components of the problem (x-direction and y-direction).

To do that, we put our 0 of coordinates where the collision takes place.

So, for the initial momentum we have that

`p_(ix)=m_(a)v_(0a)+0`

`p_(iy)=0+m_(b)v_(0b)`

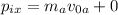
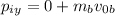
Now, this is equal to the final momentum (in each coordinate)

`p_(fx)=(m_(a)+m_(b)) v_(fx)`

`p_(fy)=(m_(a)+m_(b)) v_(fy)`

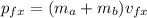
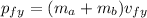
So, we equalize each coordinate and get each final velocity

`m_(a)v_(0a)=(m_(a)+m_(b)) v_(fx) \Leftrightarrow v_(fx)=(m_(a)v_(0a))/((m_(a)+m_(b)))`

`m_(b)v_(0b)=(m_(a)+m_(b)) v_(fy) \Leftrightarrow v_(fy)=(m_(b)v_(0b))/((m_(a)+m_(b)))`

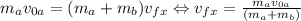
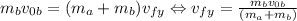
Finally, to calculate the magnitude of the final velocity, we need to calculate

`v_(f)=\sqrt{(v_(fx))^(2)+(v_(fy))^(2)}`

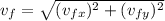
which, replacing with the previous results, is

`v_(f)=\sqrt{(v_(fx))^(2)+(v_(fy))^(2)}=(\sqrt{((18.5*8.15)/(49))^(2)+((30.5*5.00)/(49))^(2)})(m)/(s)`

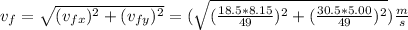
Therefore, the outcome is

`v_(f)=4.37(m)/(s)`

Answer 2

v =4.36 m/s

Step-by-step explanation:

given,

mass of object A = 18.5 Kg

initial velocity of object A = 8.15 m/s in east

mass of object B = 30.5 kg

initial velocity of object B = 5 m/s

`P = P_A+P_B`

`P = m_Av_A\widehat{i} + m_B v_B\widehat{j}`

`P = 18.5* 8.15 \widehat{i} + 30.5* 5\widehat{j}`

`P = 150.775 \widehat{i} + 152.5 \widehat{j}`

`P = √(150.775^2+152.5^2)`

P = 214. 45 N s

velocity after collision is equal to

`v =(214.45)/(18.5+30.5)`

v =4.36 m/s

hence, velocity after collision is equal to 4.36 m/s