Answer:
The magnitude of the final velocity of the two-object system is
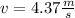
Step-by-step explanation:
As the Momentum is conserved, we can compare the instant before the collision, and the instant after. Also, we have to take in account the two components of the problem (x-direction and y-direction).
To do that, we put our 0 of coordinates where the collision takes place.
So, for the initial momentum we have that
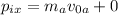
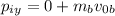
Now, this is equal to the final momentum (in each coordinate)
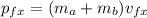

So, we equalize each coordinate and get each final velocity
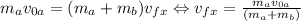
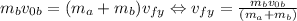
Finally, to calculate the magnitude of the final velocity, we need to calculate
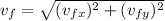
which, replacing with the previous results, is
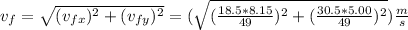
Therefore, the outcome is
