Answer:
A) P1=2 [bar] , W=-12 [kJ]
B) P1=0.8 [bar] , W=-7.3303 [kJ]
C) P1=0.6077 [bar] , W=-6.4091 [kJ]
Step-by-step explanation:
First, from the problem we know the following information:
V1=0.1 m^3
V2=0.04 m^3
P2=2 bar =200 kPa
The relation PV^n=constant means PV^n is a constant through all the process, so we can derive the initial pressure as:
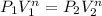
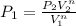
a) To the case a) the constant n is equal to 0, we can calculate the initial pressure substituting n=0 in the previous expression, so:
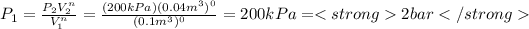
The expression to calculate the work is:
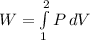
If n=0:
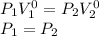
Then:
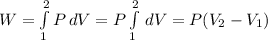
The work is:
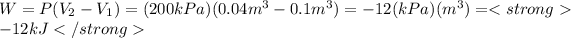
b) To the case b) the constant n is equal to 1, we can calculate the initial pressure substituting n=1 in the initial expression, so:
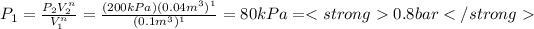
If n=1 then:
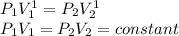
To calculate the work:
![[tex]W=constant\int\limits^2_1 {(1)/(V) } \, dV](https://img.qammunity.org/2020/formulas/physics/college/g88nycktl0izquqt6rqhg5015t2juf2g9y.png) [/tex]
[/tex]
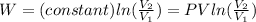
Substituting:
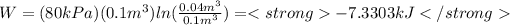
c) To the case c) the constant n is equal to 1.3, we can calculate the initial pressure substituting n=1.3 in the initial expression, so:
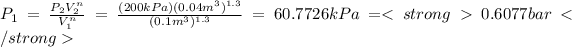
First:
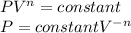
The work:
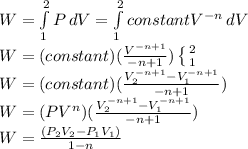
Substituting:
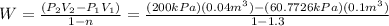
W=-6.4091 kJ